Quantum physics 1
or
Light on the photon
or
Light on the photon
Introduction
Quantum theory is used by physicists to take account of phenomena which happen at the microsopic scale of particles.
The
intrinsic power of this physics is considerable. It has potential to be
used by nuclear physicists, atomic physicists, material physicists and
even astrophysicist. To date, no experiment has come to contradict its
predictions, strange though they are. Quantum physics uses concepts which
don't always have a counterpart in daily life, you mustn't be surprised
if certain of these predictions run strenuously counter to common sense.
Albert Einstein, for example, never accepted certain consequences
of quantum theory: see how he pokes out his tongue!
Why
"quantum"?
Quantum
physics literally means "the physics of quanta" (= latin plural
of "quantum" which means quantity).
This new word appeared in the physics register on the 14th December
1900 thanks to a revolutionary paper read out before the Prussian Academy
of Sciences by the german Max Planck: He postulated the original
idea according to which, the energy exchanges between light and matter
cannot happen except in discrete packets, which he called quanta. He then
renounced the sacred law of continuity, the pillar of classical physics.
What
is "classical" and continuous light ?
Not so
easy to represent such an immaterial concept!
At the end of the XIXth century, James
Maxwell defined light as being a beam of electromagnetic waves
moving at a constant speed in the vacuum: the famous speed c of
300.000 kilometers per second.
As easy as it is to imagine a wave running across the surface of water
and sound as being a vibration in air, the concept of an electromagnetic
wave (as being an oscillation of the electric and associated magnetic field)
can leave us perplexed. How can we imagine these fields working so intimitely
together? What is there to support this oscillation in a vacuum?
Light is always characterised by its frequency or its wavelength.
Visible light is in fact nothing but a narrow window on the whole of the
spectrum of electromagnetic waves (which also include gamma rays, X rays,
ultraviolet, infrared and radio waves).See ( spectrum)
Photonic
and quantic light
After
Max Planck, this radically new notion of "quantic light" would be taken
up in 1905 by Albert Einstein who supported the idea that the energy
of light is in some ways "granularised". This "grain of electricity" would
be named photon in 1926: A new particle is born, a non-material
particle without mass.
Each photon of a radiation (light, radio waves, X rays...) carries
a quantum of energy characteristic of its frequency (frequency of visible
light = colour).
Quantum physics then associates a wave and a particle. This association
would be generalised from this to all particles, and notably the electron.
But how to reconcile a continuum (waves) with the discontinuous (particles)?
This all comes down to the wave-particle duality paradox.
Wave-particle
duality
The most important question that quantum physics has been compelling to address, concerns the manner in which to represent physical objects and their properties. The old physics, known as classical, distinguished two types of fundamental entities:
The
following analogy should help us:
Look at a cylinder from two different angles, a cylinder appears sometimes
as a circle, sometimes as a rectangle. When in fact it is neither one nor
the other.
Thats the way the photon, the electron and all elementary particles
are, thus the image of a particle is but one facet of a more complex entity.
This precise point can pose a very troubling philosophical problem:
Objective reality (if it exists independantly of the human spirit), is
it accessible? Or are we condemned to observe nothing but a world of deceptive
appearances?
Where's
light come from?
Quantum physics allows us to better understand how light is emitted
by matter...
The world of the atom according to Niels Bohr was a model at the frontier
of two ages: the classical age, pre-quantum and the quantum world. But
it already explained the mechanism of the emission of light by an atom.
:
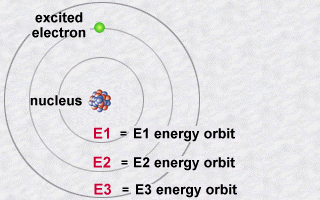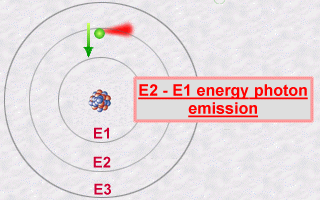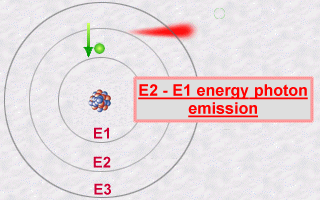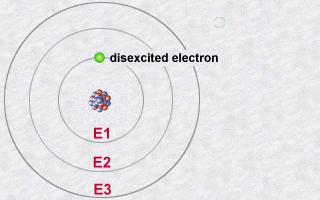
This emission is explained then by the jump which an electron makes
from an orbit E2 to an orbit E1. During this jump towards this less energetic
orbit E1 (an inner orbit), the electron will lose part of its energy in
the form of a photon emitted outwards.
The energy of this photon, E2 - E1, will be a whole number multiple (the famous quantification of light) of the value hn.
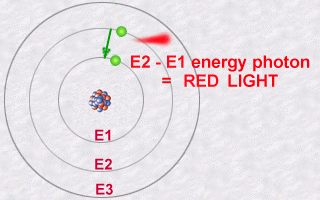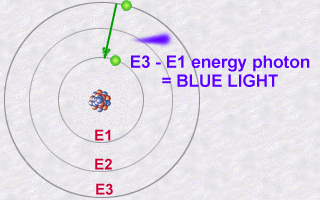
Conversely, an atoms electron could absorb a photon of a given energy and thus jump from a less energetic orbit to a more energetic orbit: It will thus become more excited than normal because it is in a more energetic orbit. It is in becoming less excited that it should subsequently re-emit a photon.
Quantum
theory stipulates that not all electronic orbits are allowed. Orbits are
not permitted unless, in jumping from one orbit to another, an electron
can emit or absorb a photon with an energy which is an exact multiple of
the famous value hn. It's this
quantic discontinuity of the energy exchange which enforces a disconuity
in the orbits which are permitted. Each permitted electronic orbit will
therefore be quantified and characterised by the quantum numbers
(4 numbers designated n, l, m t s).
For example, the number n is called the principal quantum number.
It designates the number of the electron layer also designated by the letters
K, L, M, O, P, Q.
Each atom can only emit a precise and characteristic set of colours:
Each colour of light is in fact a particular frequency (and therefore a
level of energy) of a photon. All of the possible jumps between orbits
which an electron can make within a given atom translate into the emission
(or absorption) of a characteristic spectrum of light: Here we have
a veritable identity card for a given type of atom. It's because of this
readily identifiable spectrum that we can know which atoms exist in stars
in the firmament. Their light is captured by telescopes, analysed and compared
with the spectrums of hydrogen, helium etc...
